ATM: Zaczynamy

Na tej stronie znajdziecie garść porad, króre mogą się przydać w podjęciu decyzji: kupić, czy budować samemu swój wymarzony instrument, oraz czym się kierować w jego wyborze.

1. Zanim kupisz teleskop:

• występowała okropna aberracja sferyczna - obraz w kierunku brzegów pola widzenia bardzo tracił ostrość
• osie optyczne obiektywów były źle skolimowane: oba obiektywy patrzyły w rózne strony i obraz był rozdwojony
• na obudowie pisało 20x50: o ile średnica obiektywu była zgodna z prawdą (50 mm), to deklarowane powiększenie 20x już nie: nawet na oko było widać, że źrenica wyjściowa lornetki wyrażona średnicą plamki światła w okularze (lornetka skierowana w niebo) miała średnicę około 5 mm, czyli faktyczne powiększenie mogło wynosić około 10x (50 mm średnicy obiektywu podzielone przez średnicę krążka światła w okularze, tu: 5 mm = 10x). Gdyby lornetka ta miała faktyczne powiękzenie 20x, wtedy ten krążek musiał by mieć średnicę 2,5 mm!

2. Kupić czy budować?

3. Jaki instrument wybrać?

Przy tej samej średnicy obiektywu i jakościowo dobrym obiektywie, to luneta daje obrazy bardziej ostre i klarowne - słowem - lepsze, a to z uwagi na brak centralnie położonego lusterka wtórnego, które zawsze daje dodatkowe rozproszenie i ugięcie światła, psujące nieco kontrast i ostrość. Ale, niestety, jest droższa. Z drugiej jednak strony, teleskop zwierciadlany jest tańszy i z natury pozbawiony aberracji chromatycznej, a to po prostu oznacza, że obraz będzie wolny od barwnych obwódek, przy założeniu, że posiadamy okular dobrej jakości. Tylko na prawdę dobre refraktory są praktycznie pozbawione tej wady, ale niestety, to teleskopowa arystokracja, ceny raczej nie dla zwykłych śmiertelników :-(.
Ale nie zrażajmy się! Ciekawym i rozsądnym cenowo rozwiązaniem tego impasu (chcemy mieć wysokiej klasy instrument o dużej średnicy obiektywu, a cenowo był by nie do przeskoczenia, gdyby był apochromatycznym refraktorem) wydaje się teleskop Lurie - Houghton (w dużym uproszczeniu jest to Newton z lustrem sferycznym i optyką korygujacą komę, wykonaną z 2 płyt ze szkła BK7, znakomity optycznie, o parametrach nie gorszych od apochromatycznego refraktora!!! Zajrzyjcie koniecznie: http://members.cox.net/rmscott/lh_scope/index.html:
Teleskop zwierciadlany, w tym konstrukcyjnie prosty (a więc tani i łatwy do wykonania!) teleskop Newtona może być całkiem przyzwoitej klasy instrumentem za przystępną cenę. Jako przykład mozna podać koszt budowy teleskopu Newtona 250/1250 mm na montażu Dobsona, który wyniósł około 1600 zł. Za tę cenę można było kupić gotowy teleskop Newtona (np. Mizar, TAL -1 na montażu paralaktycznym) o średnicy obiektywu 110 mm. Gotowy teleskop Newtona o średnicy lustra 250 mm i na montażu Dobsona kosztował by około dwukrotnie więcej. Sami przyznacie, że warto zbudować samemu. Kolejnym argumentem, przemawiającym za teleskopem Newtona, jest możliwość wykonania dość dużego instrumentu i o dużej światłosile, a więc szczególnie przydatnego jako szukacz komet lub do oglądania obiektów mgławicowych. Budowane są modele o światłosile nawet 1:4!
Bardzo poręczne gabarytowo są teleskopy Cassegraina w róznych odmianach , z uwagi na swoje zwarte wymiary i stosunkowo niewielką masę. Od teleskopów Newtona są droższe i trudniejsze w wykonaniu, ale cenowo w porównaniu z refraktorami są tańsze.

• zasięg instrumentu
• jego zdolność rozdzielcza
• maksymalne powiększenie użyteczne

Zasięg instrumentu:
Można go wyrazić jasnością najsłabszych dostrzeżonych gwiazd, mierzoną w magnitudo.
Zasięg instrumentu w magnitudo można w przybliżeniu sobie samemu obliczyć, wiedząc, że każdemu wzrostowi/spadkowi o 1 magnitudo towarzyszy około 2,5 krotny wzrost /spadek jasności gwiazdy (dokładnie: pierwiastek piątego stopnia z liczby 100, czyli 100 krotny wzrost jasności obiektu wyrazi się zwiększeniem jego jasności dokładnie o 5 mag). Analogicznie: 2,5 krotne zwiększenie powierzchni jego obiektywu zwiększy jego zasięj o 1 mag. Jeżeli zwiększymy powierzchnię obiektywu 100 krotnie (czyli 10 krotnie zwiększymy jego średnicę), to zasięg takiego teleskopu wzrośnie o 5 magnitudo.
Załóżmy, że gołym okiem w przeciętnych warunkach przejrzystości atmosfery (średnica źrenicy naszego oka średnio zaadaptowanego do ciemności równa 7 mm) widzimy maksimum gwiazdy 5 magnitudo. W tych samych warunkach teleskopem o średnicy obiektywu 70 mm (10 krotny wzrost średnicy, a powierzchni 100 krotny w stosunk do naszego oka, a więc zysk o 5 mag) uzyskamy zasięg 10 mag.
Zasięg ten możemy również obliczyć ze wzoru: m = 5.5 + 5 ln r/7, gdzie: r= średnica obiektywu w milimetrach. Wzór ten zakłada średnicę źrenicy oka zaadaptowanej do ciemności równą 7 mm, a zasięg widoczności gwiazd gołym okiem 5,5 mag.

Zdolość rozdzielcza:
Według jednych żródeł (np. Poradnik miłośnika astronomii Kulikowskiego)maksymalną zdolność rozdzielczą teleskopu w sekundach łuku mozna obliczyć, dzieląc 14 przez średnicę obiektywu w cm.
Wg limitu Dawes'a wynikającego z falowej natury światła, mozna go obliczyć ze wzoru: Dawes limit = 227000 x lambda/D [sekundy łuku], lambda i D [średnica obiektywu] wyrażone w cm. Limit Dawes'a (Dawes limit w ang.) jest kątowa zdolnością rozdzielcz a teleskopu, zalezną od długości fali obserwowanego światła i średnicy obiektywu). Czyli, dla lambda = 550 nm (0,000055 cm), w przybliżeniu 12,5 dzielone przez średnicę obiektywu w cm.
Ze zdolnościa rozdzielczą wiąże się średnica krązka dyfrakcyjnego (krązka Airego), który jest obrazem punktowego żródła światła. Jego liniowa średnica zalezy tylko od światłosiły teleskopu oraz długości fali światła.
Mozna ją obliczyć z prostego wzoru:

Nietrudno zauważyć, że dla dwóch teleskopów o identycznej ogniskowej, ten o większym lustrze głownym, a więc o większej światłosile (liczba F czyli stosunek średnicy do ogniskowej obiektywu - jest mniejsza!) - da mniejszą średnicę krążków Airego.
Biorąc pod uwagę obraz gwiazdy podwójnej, w przypadku mniej światłosilnych teleskopów - krązki dyfrakcyjne tworzące jej obraz mogą się zlewać, a dla bardziej światłosilnych - a więc o wiekszej średnicy obiektywu - moga być widoczne już jako oddzielone - a więc łatwiej rozdzielimy gwiazdę podwójną, co wyjaśnia rysunek:

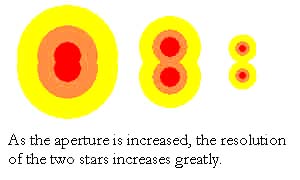
Maksymalne powiększenie użyteczne:
Jest to takie powiększenie, powyżej którego dalszy wzrost powiekszenia nie poprawia widoczności najdrobniejszych szczegółów, a tylko pogarsza ostrość.
Dla obiektywów zwierciadlanych można je obliczyć, mnożąć średnicę obiektywu w milimetrach przez 2 lub w calach razy 50. Dla wysokiej klasy refraktorów średnicę w milimetrach można nawet mnożyć przez 3. Dlatego nie dajcie się skusić dużymi powiększeniami tanich, małych teleskopów z Dalekiego Wschodu!
W powyższych założeniach zakładamy warunek, że lustro spełnia wymóg dokładności wykonania 1/8 lambda i ponad 90% światła gwiazdy mieści się w krązku dyfrakcyjnym w stosunku do teoretycznej (84% - centralny krążek, a około 16% - prążki dyfrakcyjne). Dotyczy to rzecz jasna bardzo dobrych warunków pogodowych: idealnej stabilności atmosfery. Aby można było takie powiększenie uzyskać dla danej średnicy obiektywu, obiektyw musi być dobrze wykonany (dokładność wykonania krzywizny lustra głównego: minimum 1/8 długości fali światła, mierzonej dla światła żółtozielonego, na które oko jest najbardziej wrażliwe; lambda =550 nm) oraz musi być prawidłowo wyregulowane jego położenie (justacja).

Średnica obiektywu:
Jeżeli mamy możliwość wyboru, to wybierajmy większy teleskop, przytaczając myśl z broszurki pana Rybarskiego i Serkowskiego, już klasyka ATMu: "koszt i pracochłonność budowy instrumentu o mniejszej średnicy obiektywu jest niewiele mniejszy, a wiąże się z zawężeniem zakresu obserwacji". Weźmy jednak pod uwagę to, że wraz ze wzrostem średnicy lustra rosną również gabaryty instrumentu i trudno by było się "porywać" na instrument z lustrem np. 300 mm średnicy, mieszkając w bloku. Chyba, że jest to teleskop rozbieralny, a montaż i demontaż nie zabiera wiele czasu i da się wykonać nawet pod gołym, czarnym niebem. Brać też należy pod uwagę mobilność. Druga rzecz, nie mniej ważna, tu zacytujmy Janusza Wilanda: "Budujmy taki instrument, który na pewno damy radę ukończyć".

• Teleskop "mały" - średnica obiektywu do ok. 100 mm.
  Chociaż jest to niewielki instrument, to nie zrażajmy sie tym. Ma ogromną zaletę: jest bardzo poręczny, lekki i mobilny, jak również łatwy do wykonania. Szlifowanie i polerowanie lustra głównego do takiego teleskopu jest mało pracochłonne; zdejmuje się niedużo szkła, a ponadto poleruje się je do powierzchni sferycznej. Niewielkie odchyłki od powierzchni sferycznej mają niewielki wpływ na jakość obrazu, dlatego też taki instrument może wykonać każdy. Takim instrumentem już można bez trudu podziwiać Księżyc z kraterami, oglądać jasne planety; tu można dojrzeć pierścień Saturna z przerwą Cassiniego, a przy sprzyjających warunkach można nawet dostrzec pasiaste chmury na tarczy planety. Bez problemu można oglądać Jowisza z pasami chmur na jego powierzchni czy 4 księżyce galileuszowe Jowisza. Spośród obserwacji, które mają wartość naukową, można wykonywać obserwacje plam na Słońcu, obserwacje jaśniejszych komet czy gwiazd zmiennych, lub zakrycia jaśniejszych gwiazd przez Księżyc, nie mówiąc o obserwacji zaćmienia Słońca czy Księżyca! Warto wspomnieć, że p. G.D. Dobrowolski z Rosji takim właśnie instrumentem prowadził obserwacje aktywności Słońca i opublikował bardzo ciekawy artykuł o dużej wartości naukowej. Można nim również obserwować jaśniejsze obiekty mgławicowe, które będą widoczne jako mgliste, rozmyte plamki, ale dla obserwacji szczegółów tych obiektów potrzeba wiekszych instrumentów.
• Jako optymalną można przyjąć średnicę obiektywu 12 - 15 cm.
  Przy światłosile 1:8 da ogniskową 100-1200 mm. Lustro sferyczne dla światłosiły 1:8 i średnicy obiektywu 120-150 mm spełnia jeszcze minimalny warunek 1/4 lambda, ale tu sfera musi być dokładnie wykonana, aby nie wyjść poza tę granicę. Można też wykonać instrument "krótszy", ale należy pamiętać o tym, że musi mieć już powierzchnię paraboliczną, trudniejszą do wykonania. Takim instrumentem zobaczymy większość obiektów mgławicowych, bez problemu jaśniejsze komety, nie mówiąc o Księżycu i planetach. Jest to nadal instrument mobilny i poręczny, a zasięg i możliwości całkiem spore: można nim obserwować komety o jasności do około 10 mag, gwiazdy do ok. 12-13 mag, zakrycia i odkrycia gwiazd do około 9,5 mag. Jako instrument szczególnie dedykowany do obserwacji planet i dość łatwy w budowie z uwagi na lustro sferyczne, polecamy instrument 150/1500 mm. Sfera dla tego lustra posiada odchyłkę od paraboli około 1/8 lambda, czyli jest już to bardzo dobre lustro. Ma on dośc dużą ogniskową, co pozwoli na łątwe uzyskiwanie dużych powiększeń, a mała światłosiła gwarantuje bardzo dobrą, wyrównaną ostrość w całym polu widzenia.
• Dla bardziej wymagających można polecić "kaliber " w przedziale 15-20 cm.
  Tu już dostępne jest wiele obiektów "głębokiego nieba", słabsze komety. Jeżeli wykonamy instrument 200 mm o światłosile 1:5 (ogniskowa 1000 mm), to mimo całkiem przystępnych gabarytów (tubus będzie miał długość około 110 cm) będzie to wspaniały szukacz komet, nie mówiąc już o zakryciach gwiazd nawet 10 mag! Najjaśniejsze obiekty głębokiego nieba ukażą nam swoją strukturę. Jednak należy pamiętać, że lustro do takich teleskopów musi miec powierzchnię paraboliczną, o wiele trudniejszą w wykonaniu, niz sferyczna. Ale nie nalezy sie tym zrażać: po prostu można wyszlifować i wypolerować lustro na sferę, a nadanie kształtu parabolicznego powierzyć fachowcowi - Jerzemu Poruczce quasarpj@teleskopy.pl), lub też zakupić u nich gotowe.
• 250 mm i większe:
  Takie "armaty" buduje się z reguły z myślą o astrofotografii, kometach i obiektach mgławicowych, nawet tych słabszych. Z reguły są to instrumenty o dużej światłosile, choćby z uwagi na poręczność. Dla przykładu, teleskop 300 mm o światłosile 1:6 ma ogniskową 1800 mm, i taką też w przybliżeniu długość bedzie miał tubus tego urządzenia. Instrument taki zbiera dużo światła, a więc umożliwia wydatne skrócenie czasu ekspozycji zdjęcia. Poza tym, nawet dla dużych powiększeń, spadek jasności jest mniejszy w porównaniu z instrumentami o mniejszej średnicy obiektywu przy tej samej długości ogniskowej (o mniejszej światłosile).
  Nie zalecamy ich budowy początkującym miłośnikom astronomii. Nie dlatego, że nie dali by rady ich zbudować. Nie jest to aż takie trudne, by sobie nie mogli dać z nimi rady. Powód leży gdzie indziej. Otóz początkujący nie mają zbyt dużego doświadczenia obserwacyjnegoi i jeszcze nie za bardzo wiedzą, czego oczekiwać od tak dużego i silnego instrumentu, po prostu nie wykorzystają w pełni jego zalet i mogą być nieco rozczarowani. Są to jednak instrumenty duże, a przez to mniej mobilne. Wymagają one również bardziej solidnej konstrukcji tubusa oraz potrzebują więcej czasu na ich wykonanie. Nie nalezy się jednak tym zrażac. Jezeli jesteśmy pewni, że akurat taki instrument jest nam potrzebny, posiadamy dużą chęc i wolę walki, to warto, a nawet należy się uprzeć, a na pewno się uda!

C. OGNISKOWA I ŚWIATŁOSIŁA:
Im dłuższa ogniskowa, tym większe powiększenia możemy uzyskać dla danego okularu. Na przykład teleskopem o ogniskowej 1250 mm i okularze 25 mm uzyskamy powiększenie 50x (1250:25=50). Zwiększając ogniskową do 1500 mm, tym samym okularem uzyskamy powiększenie 60x.
Światłosiła wyraża się stosunkiem średnicy obiektywu do jego ogniskowej, np. teleskop o ogniskowej 1250 mm i średnicy lustra 250 mm będzie miał światłosiłę 1:5. Im większa światłosiła, czyli zdolność zbierania światła ("jasność") obiektywu, tym większy zasięg teleskopu przy tej samej ogniskowej, ponieważ wzrośnie średnica obiektywu. Przykładowo zwiększając światłosiłę teleskopu dla tej samej ogniskowej do 1:4, nowy obiektyw będzie mieć średnicę około 312 mm. Nie należy jednak z tym przesadzać, należy pamiętać, że wraz ze wzrostem światłosiły nieuchronnie rośnie proporcjonalnie aberracja sferyczna, i to do 3 potęgi! Zatem jeżeli zwiększymy światłosiłę dwukrotnie z 1:10 do 1:5 to aberracja sferyczna urośnie 8 krotnie! Dla teleskopu Newtona o światłosile 1:10 całe pole widzenia będzie idealnie ostre, zaś dla 1:5 przy brzegach pole widzenia będzie wyraźnie nieostre. Cóż, coś za coś. Dobra ostrość na całej powierzchni pola widzenia występuje dla światłosił do około 7. Poza tym zjawisko to dla teleskopów Newtona wyjaśnia istnienie jeszcze jednej wady: komy. Koma kątowa = r * 172/(f*(4N)2)
gdzie: r : odległość od osi w płaszczyźnie ogniskowej, N : światłosiła, f : ogniskowa.
Łatwo zauważyć, że koma jest wprost proporcjonalna do światłosiły: im większa światłosiła, tym wieksza koma i rośnie wprost proporcjonalnie do drugiej potęgi!
W przypadku obiektywu 250mm, lustra parabolicznego f/6, koma kątowa w odległości 5 mm od osi optycznej będzie mieć w przybliżeniu 3.5 sekund łuku.
Wraz ze wzrostem światłosiły rośnie również zdolność rozdzielcza, patrz rysunek powyżej.

Z praktycznego punktu widzenia
- teleskopy o małej swiatłosile bardziej odpowiednie będą do oglądania planet z uwagi na dłuższą ogniskową, a więc łatwiej będzie uzyskać duże powiększenia, poza tym obraz jest ostry w całym polu widzenia.
- Światłosilne teleskopy, o krótszej ogniskowej, ale za to większym obiektywie będą bardziej odpowiednie do oglądania obiektów rozmytych, o małej jasności powierzchniowej, a także do astrofotografii. Po prostu instrumenty te zbierają więcej światła, i mają większe pole widzenia. Relatywnie mniejsza ogniskowa tych instrumentów ułatwia stosowanie mniejszych powiększeń - a więc i większego pola widzenia, a poza tym, generalnie - obiekty rozmyte łatwiej dostrzec przy małym powiększeniu i widoczne będą jako jaśniejsze. Takimi obiektami są komety i mgławice.
Rozgraniczenie to nie jest sztywne, i nie należy martwić się tym, że teleskop o małej światłosile nie będzie nadawał się dobrze do obserwacji mgławic, a krótkoogniskowy i światłosilny do obserwacji planet. Dla teleskopu o małej światłosile użyjmy jak najmniejszego powiększenia, a światłosilny można wyposażyć w soczewkę Barlowa, wydłużającą wypadkową ogniskową układu optycznego. Planety maja małą średnicę katową, a więc nawet nieostrość na brzegach pola widzenia nie będzie aż tak bardzo przeszkadzać. Jako przykład można przytoczyć teleskop 250/1250 mm. Przy użyciu soczewki Barlowa z powodzeniem można oglądać pasy na Jowiszu, a przy idealnych warunkach pogodowych można zobaczyć koncentryczną budowę pierścienia Saturna przy powiększeniu około 500x! Nawet bez soczewki Barlowa, przy px125, Księżyc ukazuje mnóstwo fantastycznych szczegółów przy fenomenalnej wręcz ostrości!
I na odwrót, przy powiększeniu 60x, w dobrym refraktorze 81/1200 mm (światłosiła około 1:15, obiektyw Fraunhofera) wspaniale widać M42 w Orionie jako delikatny, zwiewny motyl. O dziwo, mgławica M 57 w Lutni prezentowała się nawet lepiej, niż w teleskopie Newtona 110/805 mm!

D. MONTAŻ:
Najprostszy do wykonania i zarazem najtańszy jest montaż azymutalny typu Dobsona. Mimo z pozoru topornego wyglądu (drewniana, obrotowa skrzynia podstawy, a teleskop wygląda w niej jak armatka na XVII wiecznym okręcie), to w prównaniu ze zgrabniejszym odeń trójnogiem, Dobson jest prosty, trwały i niezawodny, a przy tym sztywny i mało podatny na drgania, co sprawia, że chętnie jest stosowany przez miłosników astronomii, zwłaszcza do posadzenia na nim instrumentów większego "kalibru". Dobrze wykonany i wyważony, o prawidłowo dobranych tarciach na łożyskach, pozwala na wygodne i bardzo łatwe skierowanie instrumentu na dowolny fragment nieba. Przy odrobinie wprawy z prowadzeniem instrumentu można obserwować z powodzeniem zakrycia i odkrycia gwiazd przez Księżyc, czy zakrycia planetoidalne.
Montaż paralaktyczny: jest trudniejszy i droższy w wykonaniu. Im lepszy, tym droższy, z uwagi na konieczność uzyskania sztywności konstrukcji samego montażu oraz braku luzów na łożyskach, jak również konieczność wysokiej precyzji wykonania przekładni, to niezależnie od klasy wykonania, bezsporną zaletą montażu paralaktycznego (równikowego, ekwatoriału) jest możliwośc prowadzenia teleskopu za ruchem nieba, a praktycznie: gwiazda nie zjeżdża z pola widzenia i nie występuje rotacja pola widzenia. Przy dokładnym zgraniu osi rektascensji (osi godzinnej) z osią obrotu Ziemi (oś ta skierowana dokładnie w kierunku biegunów nieba) możliwe jest utrzymanie obiektu dokładnie w tym samym miejscu pola widzenia. Idealny jest więc do prowadzenia obserwacji zwłaszcza przy dużych powiększeniach, jak również do astrofotografii. Poza tym dłuższa obserwacja jednego obiektu odbywa się w warunkach komfortowych dla oka - nie trzeba wciąż poprawiać położenia obiektu w polu widzenia, co przy dużych powiększeniach jest sprawą wręcz nieodzowną.
Najlepiej wybrać taki, który jako minimum posiada napęd ręczny (mikroruchy) w obu osiach: deklinacji i rektascensji. Wskazane jest, aby posiadał napęd elektryczny lub zegarowy, ale to podnosi cenę.